Matrix Calculator Perform matrix operations: add, multiply, find determinant, inverse, and transpose for 2×2 and 3×3 matrices.

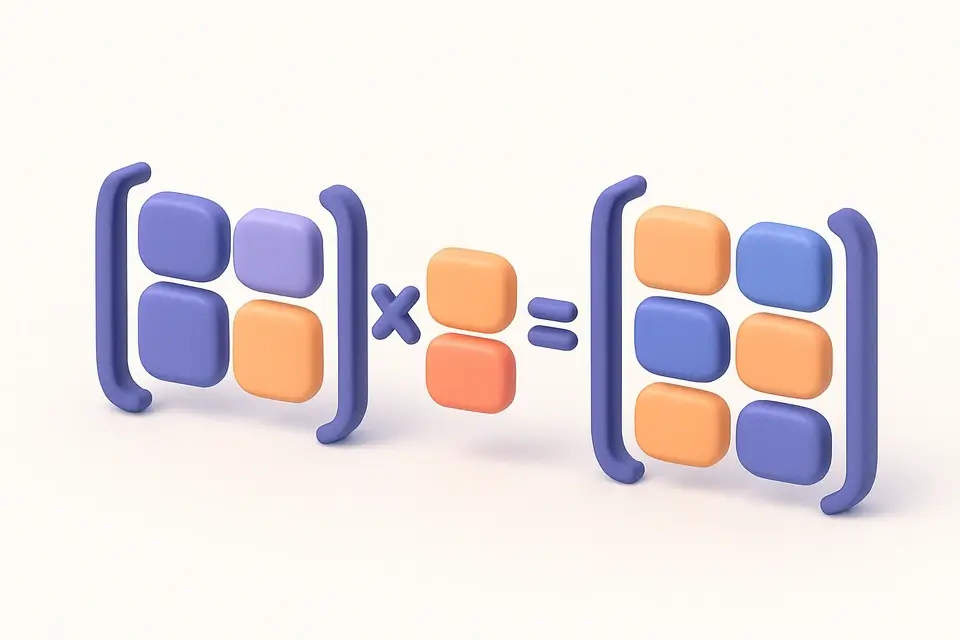
$Matrix Calculator illustration$

🔢

Matrix Calculator

Perform matrix operations: add, multiply, find determinant, inverse, and transpose for 2×2 and 3×3 matrices.

Choose Matrix Size

Select 2×2 or 3×3 matrix dimensions for your calculation.

Select Operation

Pick from add, subtract, multiply, determinant, inverse, or transpose.

Enter Matrix Values

Fill in the matrix cells with your numbers. For binary operations, fill both Matrix A and Matrix B.

Loading tool...

What Is Matrix Calculator?

A matrix calculator performs arithmetic and algebraic operations on matrices — rectangular arrays of numbers used extensively in linear algebra, computer graphics, physics, statistics, and engineering. This tool supports both 2×2 and 3×3 matrices with six core operations: addition and subtraction (element-wise), multiplication (row-by-column dot products), determinant (a scalar value that indicates whether the matrix is invertible), inverse (the matrix that when multiplied by the original gives the identity matrix), and transpose (swapping rows with columns). Matrix math is fundamental to 3D transformations in games and CAD software, solving systems of linear equations, statistical regression, quantum mechanics, and machine learning algorithms. While doing matrix multiplication by hand is tedious and error-prone, this calculator handles all the arithmetic instantly, including the cofactor expansion method for determinants and the adjugate method for finding inverses.

Why Use Matrix Calculator?

Supports all essential matrix operations in one tool
Handles both 2×2 and 3×3 matrix sizes
Detects singular matrices (determinant = 0) when computing inverse
Clean visual matrix layout for easy data entry
Instant computation — no waiting or server round-trips

Common Use Cases

Linear Algebra Coursework

Check matrix homework problems including multiplication, determinants, and inverse calculations.

Computer Graphics

Compute transformation matrices for rotation, scaling, and translation in 2D/3D graphics.

Systems of Equations

Use matrix inverse or determinant to solve systems of linear equations.

Data Science

Understand matrix operations underlying PCA, regression, and other statistical methods.

Technical Guide

Matrix operations follow strict rules based on matrix dimensions. Addition and subtraction are element-wise: (A ± B)[i][j] = A[i][j] ± B[i][j], requiring matrices of the same size. Matrix multiplication uses the row-by-column dot product: (AB)[i][j] = Σ(A[i][k] × B[k][j]) for k = 1 to n. Note that matrix multiplication is NOT commutative (AB ≠ BA in general). The determinant for a 2×2 matrix [a,b;c,d] is ad − bc. For 3×3, it uses cofactor expansion along the first row: det(A) = a(ei−fh) − b(di−fg) + c(dh−eg). A matrix is invertible only when its determinant is non-zero. The inverse of a 2×2 matrix [a,b;c,d] is (1/det) × [d,−b;−c,a]. For 3×3, the calculator computes the matrix of cofactors, transposes it (adjugate), and divides by the determinant. Transpose simply swaps rows and columns: A^T[i][j] = A[j][i]. All results are displayed with up to 4 decimal places for readability.

Tips & Best Practices

1
Matrix multiplication is not commutative — A×B usually differs from B×A
2
A determinant of 0 means the matrix is singular (not invertible)
3
For a 2×2 matrix, the inverse formula is straightforward: swap diagonals, negate off-diagonals, divide by determinant
4
The transpose of a product equals the product of transposes in reverse order: (AB)^T = B^T × A^T
5
The identity matrix (1s on diagonal, 0s elsewhere) is the matrix equivalent of the number 1

Related Tools

$Scientific Calculator - free online tool$

Scientific Calculator

Full-featured scientific calculator with trigonometry, logarithms, factorials, and more.

🔢 Math & Calculators

$Quadratic Equation Solver - free online tool$

Quadratic Equation Solver

Solve quadratic equations (ax² + bx + c = 0) and find roots, discriminant, and vertex.

🔢 Math & Calculators

$Number Base Converter - free online tool$

Number Base Converter

Convert numbers between any bases from 2 to 36, including binary, octal, decimal, and hex.

🔢 Math & Calculators

$Prime Factorization - free online tool$

Prime Factorization

Find the prime factors of any number with expanded form and divisor count.

🔢 Math & Calculators

Frequently Asked Questions

Q What is a matrix determinant used for?

The determinant tells you if a matrix is invertible (det ≠ 0), gives the scaling factor of the linear transformation, and is used in solving systems of equations via Cramer's rule.

Q Why can't I find the inverse of my matrix?

If the determinant is zero, the matrix is singular and has no inverse. This means the rows (or columns) are linearly dependent.

Q What is the difference between 2×2 and 3×3 operations?

The operations are the same conceptually, but 3×3 matrices involve more computation. Determinant calculation goes from 2 terms to 6, and inverse requires 9 cofactors instead of 4.

Q Can I multiply matrices of different sizes?

This calculator works with square matrices of the same size. In general, you can multiply an m×n matrix by an n×p matrix to get an m×p result.

Q What is a transpose used for?

Transposing swaps rows and columns. It's used in linear algebra proofs, computing symmetric matrices, and is essential in least-squares regression (A^T × A).

About This Tool

Matrix Calculator is a free online tool by FreeToolkit.ai. All processing happens directly in your browser — your data never leaves your device. No registration or installation required.