Skip to main content
FreeToolkit .ai

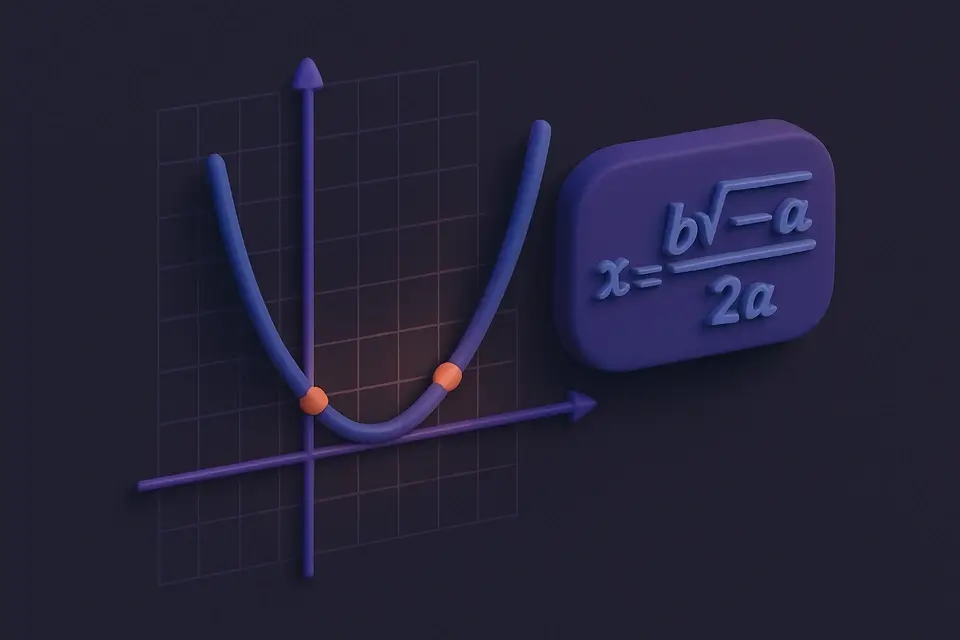
Quadratic Equation Solver Solve quadratic equations (ax² + bx + c = 0) and find roots, discriminant, and vertex.

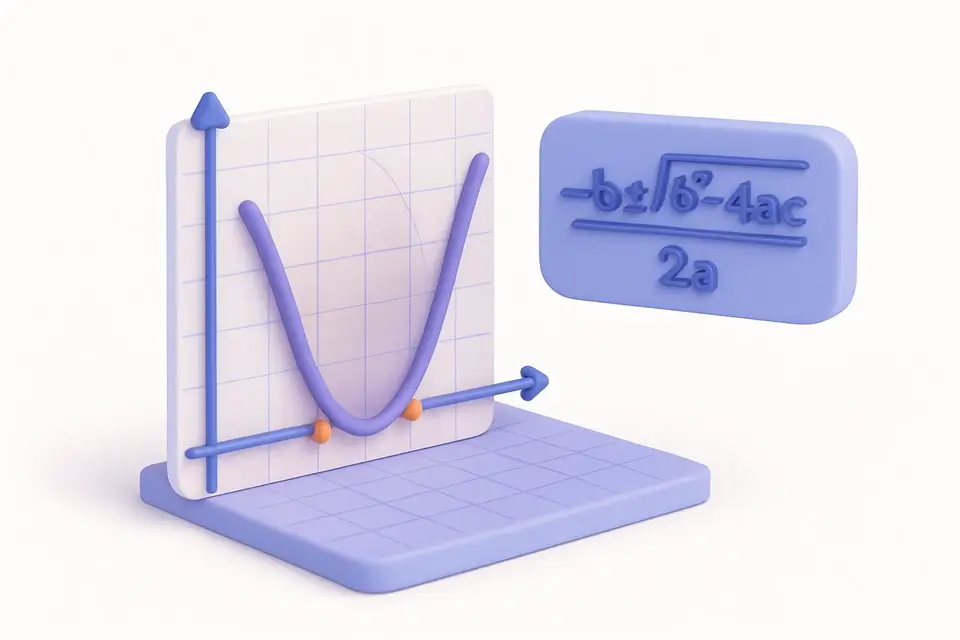
Quadratic Equation Solver illustration
🔢

Quadratic Equation Solver

Solve quadratic equations (ax² + bx + c = 0) and find roots, discriminant, and vertex.

1

Enter Coefficients

Input the values for a (x² coefficient), b (x coefficient), and c (constant term).

2

View the Solution

See the roots (real or complex), discriminant value, and type of roots.

3

Check Vertex

View the vertex coordinates of the parabola defined by your equation.

Loading tool...

What Is Quadratic Equation Solver?

The quadratic equation solver finds the roots (solutions) of any equation in the form ax² + bx + c = 0 using the quadratic formula: x = (−b ± √(b²−4ac)) / 2a. The discriminant (b²−4ac) determines the nature of the solutions: when positive, there are two distinct real roots; when zero, there is one repeated real root; when negative, there are two complex conjugate roots involving imaginary numbers. Beyond finding roots, the solver also computes the vertex of the parabola y = ax² + bx + c, located at (−b/2a, c − b²/4a), which represents either the minimum or maximum point of the curve. Quadratic equations appear in physics (projectile motion), engineering (structural analysis), economics (profit optimization), and geometry (area problems). This tool handles all cases including complex roots, negative coefficients, and fractional values, displaying results with clear formatting and the applied formula.

Why Use Quadratic Equation Solver?

  • Solves any quadratic equation with real or complex roots
  • Shows discriminant to understand the nature of solutions
  • Computes vertex for parabola graphing
  • Displays the quadratic formula application step by step
  • Handles edge cases like complex conjugate roots cleanly

Common Use Cases

Algebra Homework

Quickly solve and verify quadratic equation problems from math class.

Physics Problems

Solve projectile motion equations where height or position is quadratic in time.

Optimization

Find the maximum or minimum of a quadratic function by locating the vertex.

Engineering Design

Solve quadratic relationships in circuit analysis, structural loads, and signal processing.

Technical Guide

The quadratic formula x = (−b ± √(b²−4ac)) / 2a is derived by completing the square on the general quadratic equation. The discriminant Δ = b²−4ac determines root type: Δ > 0 gives two distinct real roots, Δ = 0 gives one repeated root (the parabola touches the x-axis), and Δ < 0 gives complex conjugate roots of the form (−b/2a) ± (√|Δ|/2a)i. The vertex form of a parabola is y = a(x−h)² + k where h = −b/2a and k = c − b²/4a. When a > 0 the parabola opens upward (vertex is minimum); when a < 0 it opens downward (vertex is maximum). For numerical stability, the solver uses the standard formula directly since JavaScript's double-precision arithmetic provides sufficient precision for typical educational and engineering values. The coefficient a must be non-zero for the equation to be quadratic; when a = 0, the equation becomes linear (bx + c = 0) and the tool reports this condition. Results display up to 6 decimal places for precision while maintaining readability.

Tips & Best Practices

  • 1
    The discriminant tells you everything about the roots before you even calculate them
  • 2
    If a = 0, the equation is linear, not quadratic — use simple algebra instead
  • 3
    The vertex is always at x = −b/(2a) regardless of whether the roots are real or complex
  • 4
    For projectile motion, the vertex gives the maximum height and the time to reach it
  • 5
    Complex roots always come in conjugate pairs: if a+bi is a root, so is a−bi

Related Tools

Scientific Calculator - free online tool

Scientific Calculator

Full-featured scientific calculator with trigonometry, logarithms, factorials, and more.

🔢 Math & Calculators
Matrix Calculator - free online tool

Matrix Calculator

Perform matrix operations: add, multiply, find determinant, inverse, and transpose for 2×2 and 3×3 matrices.

🔢 Math & Calculators
Exponent Calculator - free online tool

Exponent Calculator

Calculate x raised to the power of n (xⁿ) with scientific notation output.

🔢 Math & Calculators
Weighted Average Calculator - free online tool

Weighted Average Calculator

Calculate weighted averages with dynamic data entry, showing both weighted and simple averages.

🔢 Math & Calculators

Frequently Asked Questions

Q What is the quadratic formula?
x = (−b ± √(b²−4ac)) / 2a, where a, b, and c are the coefficients of ax² + bx + c = 0. The ± means there are typically two solutions.
Q What does the discriminant tell me?
If b²−4ac > 0: two distinct real roots. If b²−4ac = 0: one repeated root. If b²−4ac < 0: two complex roots (involving the imaginary number i).
Q What are complex roots?
Complex roots involve the imaginary unit i = √(−1). They occur when the discriminant is negative, meaning the parabola doesn't cross the x-axis.
Q Can a equal zero?
No. If a = 0, the equation becomes bx + c = 0, which is linear, not quadratic. The calculator will report this error.
Q What is the vertex of a parabola?
The vertex is the turning point — the minimum point if the parabola opens upward (a > 0) or the maximum point if it opens downward (a < 0).

About This Tool

Quadratic Equation Solver is a free online tool by FreeToolkit.ai. All processing happens directly in your browser — your data never leaves your device. No registration or installation required.