二次方程求解器 解决二次方程（ax² + bx + c = 0）并找到根、判别式和顶点。

What Is 二次方程求解器?

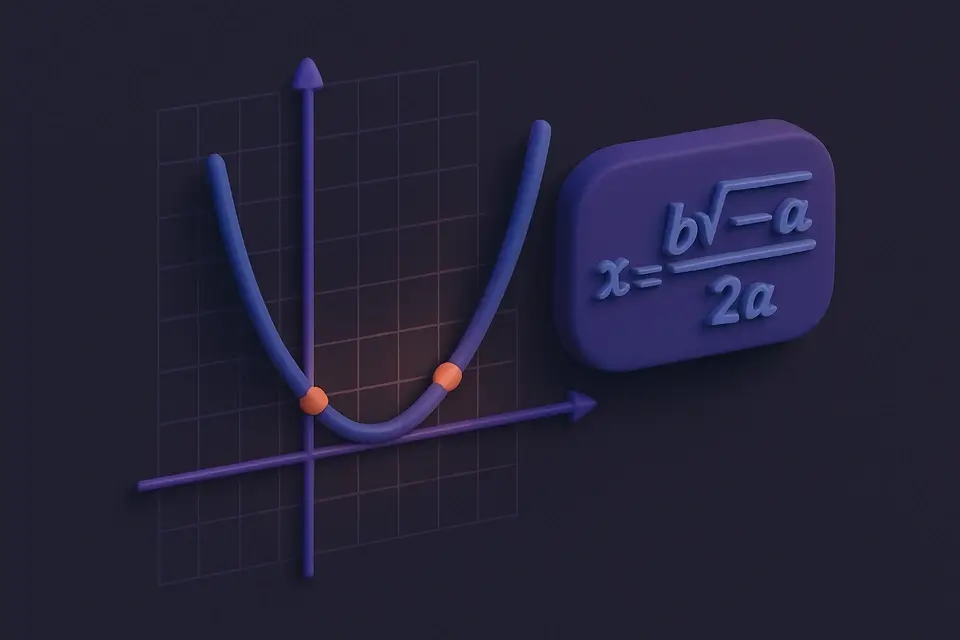
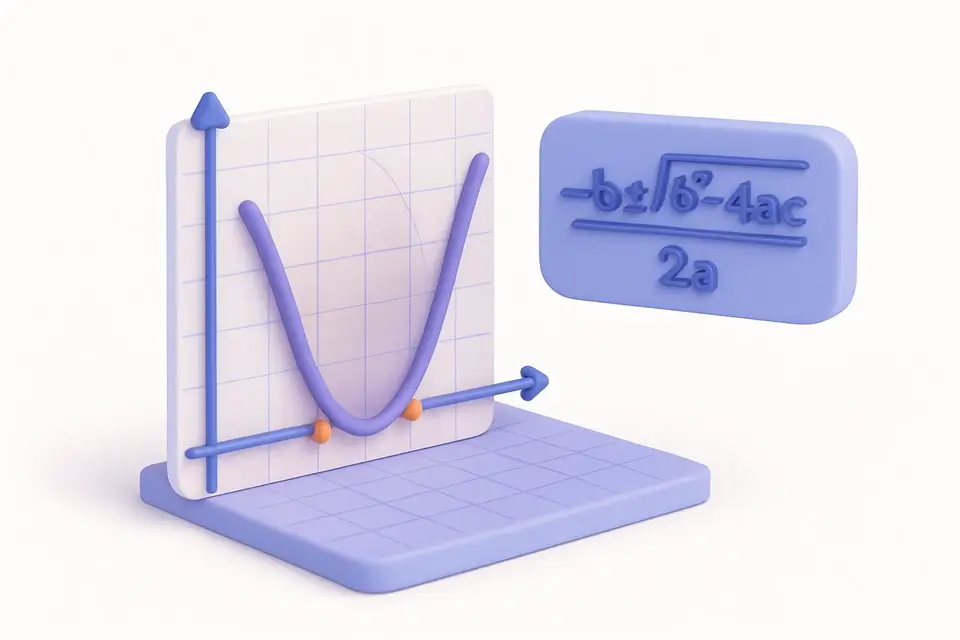
二次方程求解器使用二次公式：x = (−b ± √(b²−4ac)) / 2a，找出任何形式为ax² + bx + c = 0的方程的根（解）。判别式（b²−4ac）决定了解的性质：当它为正时，有两个不同的实根；当它为零时，有一个重复的实根；当它为负时，有两个涉及虚数的复共轭根。除了找到根之外，求解器还计算出抛物线y = ax² + bx + c的顶点，位于（−b/2a, c − b²/4a），它代表了曲线的最小或最大点。二次方程在物理学（抛物线运动）、工程学（结构分析）、经济学（利润优化）和几何学（面积问题）中都有应用。这款工具可以处理所有情况，包括复根、负系数和分数值，并以清晰的格式显示结果和所用的公式。

Why Use 二次方程求解器?

• 可以解出任意二次方程，包括实数和复数根
• 显示判别式，以了解解的性质
• 计算抛物线图形的顶点
• 逐步展示二次公式的应用
• 清晰地处理边缘情况，如复共轭根

Common Use Cases

代数作业

快速解答和验证数学课中的二次方程问题。

物理问题

解出投影运动方程，其中高度或位置是时间的二次函数。

优化

通过定位顶点找到二次函数的最大值或最小值。

工程设计

解出电路分析、结构载荷和信号处理中的二次关系。

Technical Guide

二次公式x = (−b ± √(b²−4ac)) / 2a是通过对一般二次方程完成平方而得出的。判别式Δ = b²−4ac决定了根的类型：Δ > 0给出两个不同的实根，Δ = 0给出一个重复的根（抛物线触及x轴），Δ < 0给出形式为（−b/2a）± (√|Δ|/2a)i的复共轭根。抛物线的顶点形式是y = a(x−h)² + k，其中h = −b/2a和k = c − b²/4a。当a > 0时，抛物线向上开（顶点为最小值）；当a < 0时，它向下开（顶点为最大值）。为了保证数值稳定性，求解器直接使用标准公式，因为JavaScript的双精度算术提供了足够的精度用于典型的教育和工程应用。系数a必须非零，否则方程将变成线性的（bx + c = 0），工具会报告这种情况。结果显示最多6位小数，以保持可读性。

Tips & Best Practices

• 1
  判别式可以在计算根之前告诉你关于根的一切
• 2
  如果a = 0，则方程是线性的，而不是二次的 -- 使用简单的代数代替
• 3
  顶点始终位于x = −b/(2a)，无论根是否为实数或复数
• 4
  对于投影运动，顶点给出了最大高度和到达它所需的时间
• 5
  复数根总是成对出现：如果a+bi是一个根，那么a-bi也是一个根

Related Tools

科学计算器

功能齐全的科学计算器，支持三角函数、对数、阶乘等多种运算。

🔢 Math & Calculators

矩阵计算器

执行矩阵运算：加、乘、求行列式、逆和转置，支持2×2和3×3矩阵。

🔢 Math & Calculators

指数计算器

计算 x 的 n 次方（xⁿ）并以科学计数法输出结果。

🔢 Math & Calculators

投资回报率计算器

计算投资回报率（ROI），可选年度化投资回报率用于时间比较。

🔢 Math & Calculators

Frequently Asked Questions

Q 二次公式是什么？

x = (−b ± √(b²−4ac)) / 2a，其中a、b和c是ax² + bx + c = 0的系数。±表示通常有两个解。

Q 判别式告诉我什么？

如果b²−4ac > 0：两个不同的实根。如果b²−4ac = 0：一个重复根。如果b²−4ac < 0：两个复数根（涉及虚数i）。

Q 什么是复数根？

复数根涉及虚单位i = √(−1)。它们出现在判别式为负时，这意味着抛物线不与x轴相交。

Q a可以等于零吗？

否。如果a = 0，则方程变成bx + c = 0，这是线性的，而不是二次的。计算器将报告此错误。

Q 抛物线的顶点是什么？

顶点是转折点 -- 如果抛物线向上开口（a > 0），则为最小点；如果向下开口（a < 0），则为最大点。

About This Tool

二次方程求解器 is a free online tool by FreeToolkit.ai. All processing happens directly in your browser — your data never leaves your device. No registration or installation required.