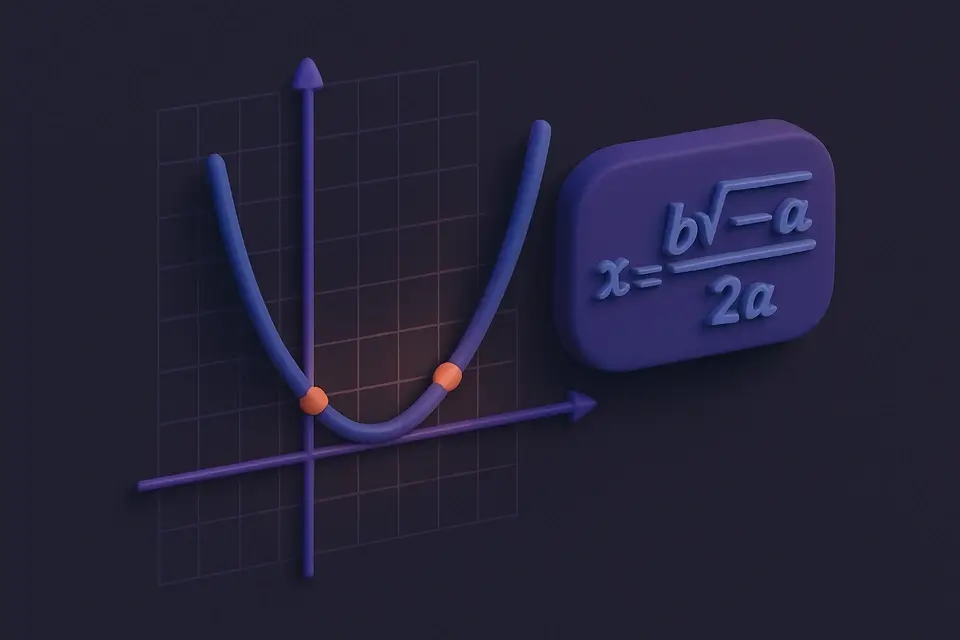
حسّاب المعادلات التربيعية حل المعادلات التربيعية (ax² + bx + c = 0) وايجاد الجذور والتمييز والمحور
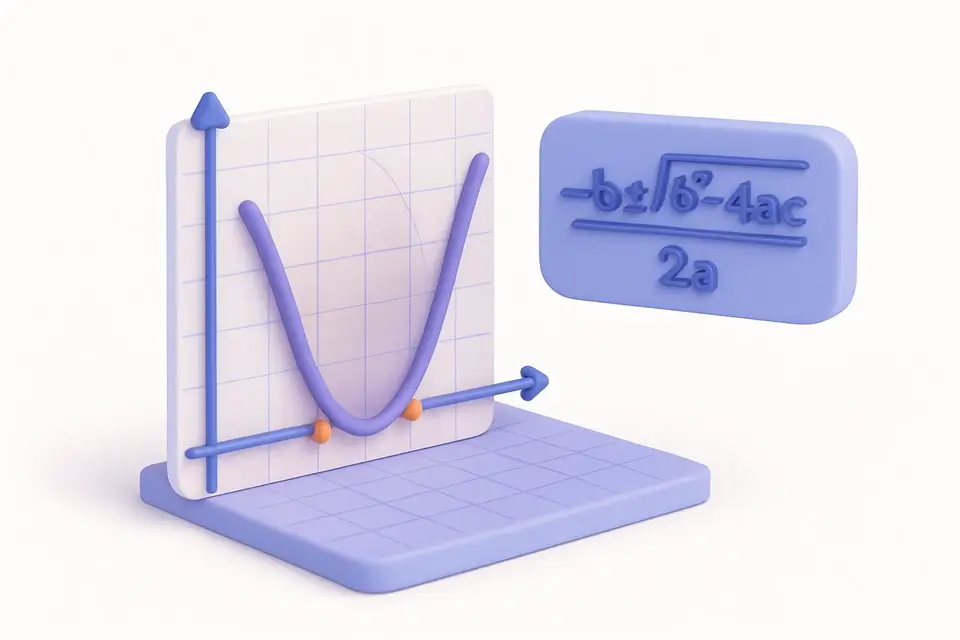
حسّاب المعادلات التربيعية
حل المعادلات التربيعية (ax² + bx + c = 0) وايجاد الجذور والتمييز والمحور
أدخل المعاملات
أدخل القيم لـ a (معامل x²)، b (معامل x)، و c (المعامل الثابت).
اعرض الحل
انظر الجذور (حقيقية أو معقدة) وقيمة التمييز ونوع الجذور.
تحقق من القمة
اعرض إحداثيات قمة المنحنى المعرف بالمعادلة الخاصة بك.
What Is حسّاب المعادلات التربيعية?
مُحَلِّل المعادلات التربيعية يجد الجذور (الحلول) لأي معادلة على شكل ax² + bx + c = 0 باستخدام الصيغة التربيعية: x = (−b ± √(b²−4ac)) / 2a. المُبَيِّن (b²−4ac) يحدد طبيعة الحلول: عند الإيجاب، هناك جذوران حقيقيان متميزان؛ عند الصفر، هناك جذر حقيقي متكرر؛ عند السالب، هناك جذران معقوفان مركبان يتضمنان أعدادًا خيالية. بخلاف إيجاد الجذور، المُحَلِّل أيضًا يحسب قمة المنحنى y = ax² + bx + c، الواقعة في (−b/2a, c − b²/4a)، والتي تمثل إما النقطة الدنيا أو العليا للمنحنى. تظهر المعادلات التربيعية في الفيزياء (حركة القذيفة)، الهندسة (التحليل الهيكلي)، الاقتصاد (تحسين الربح)، والجبر (مشاكل المساحة). هذا الأداة يتعامل مع جميع الحالات بما في ذلك الجذور المركبة، المعاملات السالبة، والقيم الكسرية، مع عرض النتائج بترتيب واضح وصيغة مطبقة.
Why Use حسّاب المعادلات التربيعية?
-
يحل أي معادلة تربيعية ذات جذور حقيقية أو معقدة
-
يوضح التمييز لفهم طبيعة الحلول
-
يحسب القمة لرسم المنحنى
-
يعرض صيغة المعادلة التربيعية خطوة بخطوة
-
يتعامل مع الحالات الخاصة مثل الجذور المركبة بشكل نظيف
Common Use Cases
واجبات الجبر
حل مشاكل المعادلات التربيعية بسرعة وتأكيد صحتها من فصول الرياضيات.
مشاكل الفيزياء
حل معادلات الحركة المقذوفة حيث يكون الارتفاع أو الموقع تربيعياً في الوقت.
التحسين
إيجاد الحد الأقصى أو الأدني للفункциة التربيعية عن طريق تحديد القمة.
تصميم الهندسة
حل العلاقات التربيعية في تحليل الدوائر والتحميل الهيكلي ومعالجة الإشارات.
Technical Guide
الصيغة التربيعية x = (−b ± √(b²−4ac)) / 2a مُشتَقَّة من إكمال المربع على المعادلة التربيعية العامة. المُبَيِّن Δ = b²−4ac يحدد نوع الجذر: Δ > 0 يعطي جذران حقيقيان متميزان، Δ = 0 يعطي جذرًا متكررًا (المنحنى يلمس محور x)، وΔ < 0 يعطي جذوران معقوفان من الشكل (−b/2a) ± (√|Δ|/2a)i. شكل القمة للمنحنى هو y = a(x−h)² + k حيث h = −b/2a وk = c − b²/4a. عندما a > 0، المنحنى مفتوح向 الأعلى (القمة هي النقطة الدنيا)؛ عندما a < 0، المنحنى مفتوح向 الأسفل (القمة هي النقطة العليا). من أجل الاستقرار الرقمي، المُحَلِّل يستخدم الصيغة القياسية مباشرةً لأن حساب JavaScript بدقة مزدوجة يوفر دقة كافية للقيم التعليمية والهندسية التقليدية. يجب أن يكون المعامل a غير صفري حتى تكون المعادلة تربيعية؛ عندما a = 0، تصبح المعادلة خطية (bx + c = 0) ويُبلّغ الأداة عن هذا الحالة. النتائج تعرض حتى 6 خانات عشرية من أجل الدقة مع الحفاظ على القراءة.
Tips & Best Practices
-
1يخبرك التمييز بكل شيء عن الجذور قبل حسابها حتى
-
2إذا كان a = 0، فإن المعادلة خطية وليست تربيعية - استخدم 代لاً بسيطة بدلاً من ذلك
-
3القمة تكون دائمًا عند x = −b/(2a) بغض النظر عما إذا كانت الجذور حقيقية أو معقدة
-
4للمسائل الحركية، تعطي القمة أقصى ارتفاع والزمن للوصول إليه
-
5الجذور المعقدة تأتي دائمًا في أزواج متكافئة: إذا كان a+bi جذراً، فإن a−bi هو أيضاً جذر
Related Tools

حاسبة علمية
حاسبة علمية متكاملة مع ثلاثيات، لوغاريتمات، факторيلات، وغيرها.
🔢 Math & Calculators
حاسبة المصفوفات
أداء عمليات المصفوفة: إضافة، ضرب، العثور على الحد الأقصى، المعكوس، والمتجه للourcem 2×2 و 3×3.
🔢 Math & Calculators
حاسبة الأسس
احسب قيمة x مرفوعة إلى степ ن (xⁿ) معخرج علمي.
🔢 Math & Calculators
مُحَوِّل العملات
قم بتحويل أكثر من 30 عملة حول العالم مع أسعار صرف تقريبية.
🔢 Math & CalculatorsFrequently Asked Questions
Q ما هي الصيغة التربيعية?
Q ماذا يخبرنا التمييز به?
Q ما هي الجذور المعقدة?
Q هل يمكن لـ a أن يساوي صفراً?
Q ما هي قمة المنحنى?
About This Tool
حسّاب المعادلات التربيعية is a free online tool by FreeToolkit.ai. All processing happens directly in your browser — your data never leaves your device. No registration or installation required.